Obliczanie logarytmu z ułamkiem może wydawać się skomplikowane, ale w rzeczywistości jest to prosty proces, który można zrozumieć dzięki kilku podstawowym zasadom. Głównym narzędziem, które ułatwia te obliczenia, jest reguła ilorazu. Dzięki niej można łatwo przekształcić logarytm z ułamka w bardziej przystępną formę, co znacząco ułatwia obliczenia.
W tym artykule przedstawimy, jak krok po kroku obliczyć logarytm z ułamków, takich jak 1/2 czy 3/4. Oprócz tego omówimy najczęstsze błędy, które mogą wystąpić podczas tych obliczeń, oraz jak ich unikać. Dzięki temu każdy, kto chce nauczyć się tej umiejętności, będzie miał solidne podstawy do dalszej pracy z logarytmami.
Najistotniejsze informacje:- Logarytm z ułamka można obliczyć, korzystając z reguły ilorazu, co upraszcza proces obliczeń.
- Przykłady obliczeń logarytmu z ułamków, takich jak 1/2 i 3/4, pokazują praktyczne zastosowanie reguły ilorazu.
- Najczęstsze błędy w obliczeniach logarytmicznych dotyczą niewłaściwego stosowania reguły ilorazu oraz błędnej interpretacji wyników.
- Umiejętność poprawnej interpretacji wyników logarytmicznych jest kluczowa dla zrozumienia ich znaczenia w matematyce.
Jak obliczyć logarytm z ułamkiem - zrozumienie podstawowych zasad
Logarytmy są kluczowym elementem matematyki, a ich zrozumienie jest niezbędne do wykonywania różnych obliczeń. Obliczanie logarytmu z ułamkiem może wydawać się trudne, ale dzięki prostym zasadom można to zrobić efektywnie. Głównym narzędziem, które wykorzystujemy do obliczeń logarytmicznych z ułamkami, jest reguła ilorazu, która pozwala na przekształcenie logarytmu z ułamka w bardziej przystępną formę.
W praktyce, aby obliczyć logarytm z ułamka, stosujemy wzór: log(a/b) = log(a) - log(b). Dzięki temu możemy łatwo obliczyć logarytm z dowolnego ułamka, co jest szczególnie przydatne w zadaniach matematycznych. Zrozumienie tych podstawowych zasad ułatwi dalszą pracę z logarytmami i pozwoli na ich efektywne wykorzystanie w różnych kontekstach.
Zasady obliczania logarytmu z ułamkiem - prosty sposób na sukces
Obliczanie logarytmu z ułamkiem opiera się na kilku kluczowych zasadach, które warto znać. Po pierwsze, logarytm z ułamka można obliczyć, stosując regułę ilorazu, co znacząco upraszcza proces. Reguła ta mówi, że logarytm z ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb. Oznacza to, że możemy rozdzielić obliczenia na prostsze części.
Po drugie, warto pamiętać, że logarytmy mają swoje podstawy, które również wpływają na wyniki obliczeń. Najczęściej spotykaną podstawą jest liczba 10 (logarytm dziesiętny) lub liczba e (logarytm naturalny). Zrozumienie, jak działają te podstawy, pomoże w lepszym zrozumieniu logarytmów i ich zastosowań w różnych dziedzinach matematyki.
Reguła ilorazu - jak wykorzystać ją w obliczeniach logarytmicznych
Reguła ilorazu stanowi fundamentalne narzędzie w obliczeniach logarytmicznych, szczególnie w kontekście obliczania logarytmu z ułamkiem. Mówi ona, że logarytm ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb. Można to zapisać matematycznie jako: log(a/b) = log(a) - log(b). Dzięki tej regule, obliczenia stają się prostsze i bardziej przejrzyste.
W praktyce, zastosowanie reguły ilorazu pozwala na łatwe przekształcenie skomplikowanych ułamków w prostsze obliczenia. Na przykład, jeśli chcemy obliczyć logarytm z ułamka 1/4, możemy to zrobić w następujący sposób: log(1/4) = log(1) - log(4). W ten sposób możemy zredukować problem do obliczenia logarytmu z liczby 1 oraz logarytmu z liczby 4, co znacznie upraszcza cały proces.
Implikacje reguły ilorazu w obliczeniach logarytmicznych
Stosowanie reguły ilorazu w obliczeniach logarytmicznych ma istotne implikacje, zwłaszcza w kontekście metody obliczania logarytmu z ułamkiem. Dzięki tej regule, możemy łatwo porównywać różne logarytmy, co jest szczególnie przydatne w analizach matematycznych i statystycznych. Pozwala to również na lepsze zrozumienie relacji między różnymi wartościami logarytmicznymi.
- Reguła ilorazu upraszcza obliczenia logarytmiczne, co jest kluczowe w matematyce.
- Umożliwia łatwe przekształcanie skomplikowanych ułamków w prostsze wartości.
- Pomaga w porównywaniu wartości logarytmicznych, co jest przydatne w analizach.
Obliczanie logarytmu z ułamka 1/2 - szczegółowy proces
Aby obliczyć logarytm z ułamka 1/2, wykorzystujemy regułę ilorazu. Zgodnie z tą regułą, możemy zapisać: log(1/2) = log(1) - log(2). Ponieważ logarytm z liczby 1 jest równy 0, proces obliczeń staje się znacznie prostszy. Zatem, mamy: log(1/2) = 0 - log(2), co upraszcza się do: log(1/2) = -log(2).
Logarytm z liczby 2, w zależności od podstawy, może być obliczany na różne sposoby. Dla logarytmu dziesiętnego, wartość ta wynosi około 0,301. Ostatecznie, obliczając log(1/2), uzyskujemy wynik: log(1/2) ≈ -0,301. Dzięki tej metodzie możemy łatwo obliczyć logarytm z ułamka, co jest niezwykle przydatne w różnych zastosowaniach matematycznych.
Przykład logarytmu z ułamka 3/4 - praktyczne zastosowanie
Obliczając logarytm z ułamka 3/4, również stosujemy regułę ilorazu. Możemy to zapisać jako: log(3/4) = log(3) - log(4). W tym przypadku musimy obliczyć logarytmy dla obu liczb. Zakładając, że korzystamy z logarytmu dziesiętnego, log(3) wynosi około 0,477, a log(4) to 0,602.
Wykonując obliczenie, otrzymujemy: log(3/4) = log(3) - log(4) = 0,477 - 0,602 = -0,125. Tak więc, logarytm z ułamka 3/4 wynosi około -0,125. Dzięki zastosowaniu reguły ilorazu, obliczenia stają się proste i zrozumiałe, co ułatwia pracę z logarytmami w różnych kontekstach.
Częste błędy przy obliczaniu logarytmu z ułamkiem - jak ich unikać
Podczas obliczania logarytmu z ułamków, wiele osób popełnia typowe błędy, które mogą prowadzić do niepoprawnych wyników. Jednym z najczęstszych błędów jest niewłaściwe stosowanie reguły ilorazu. Użytkownicy często zapominają, że logarytm z ilorazu dwóch liczb powinien być obliczany jako różnica logarytmów, a nie jako logarytm z różnicy. Warto zatem upewnić się, że stosuje się odpowiednią formułę, aby uniknąć takich pomyłek.
Innym powszechnym błędem jest mylenie podstaw logarytmu. Często zdarza się, że osoby obliczające logarytmy nie zwracają uwagi na to, jaką podstawę mają zastosować, co może prowadzić do błędnych wyników. Również, przy obliczeniach logarytmów z ułamków, niektórzy mogą nieprawidłowo interpretować wartości, co skutkuje nieprawidłowym zrozumieniem wyniku. Dlatego tak ważne jest, aby dokładnie analizować każdy krok obliczeń, aby zminimalizować ryzyko popełnienia błędów.
Najczęstsze pułapki w obliczeniach logarytmu z ułamkiem - co wiedzieć
Podczas obliczania logarytmu z ułamkami można napotkać na kilka typowych pułapek. Na przykład, wielu uczniów myli logarytm z ilorazu z logarytmem z sumy, co prowadzi do błędnych wyników. Inny błąd to pomijanie negatywnego znaku, gdy logarytm z liczby jest mniejszy od 1, co może powodować nieporozumienia w interpretacji wyników. Dodatkowo, niektórzy mogą błędnie zakładać, że logarytm z 0 jest zdefiniowany, co jest matematycznie niemożliwe. Uważne śledzenie tych typowych błędów może znacznie poprawić dokładność obliczeń logarytmicznych.
Czytaj więcej: Czemu Quo Vadis jest powieścią historyczną? Odkryj jej tajemnice
Jak poprawnie interpretować wyniki obliczeń logarytmicznych - kluczowe wskazówki
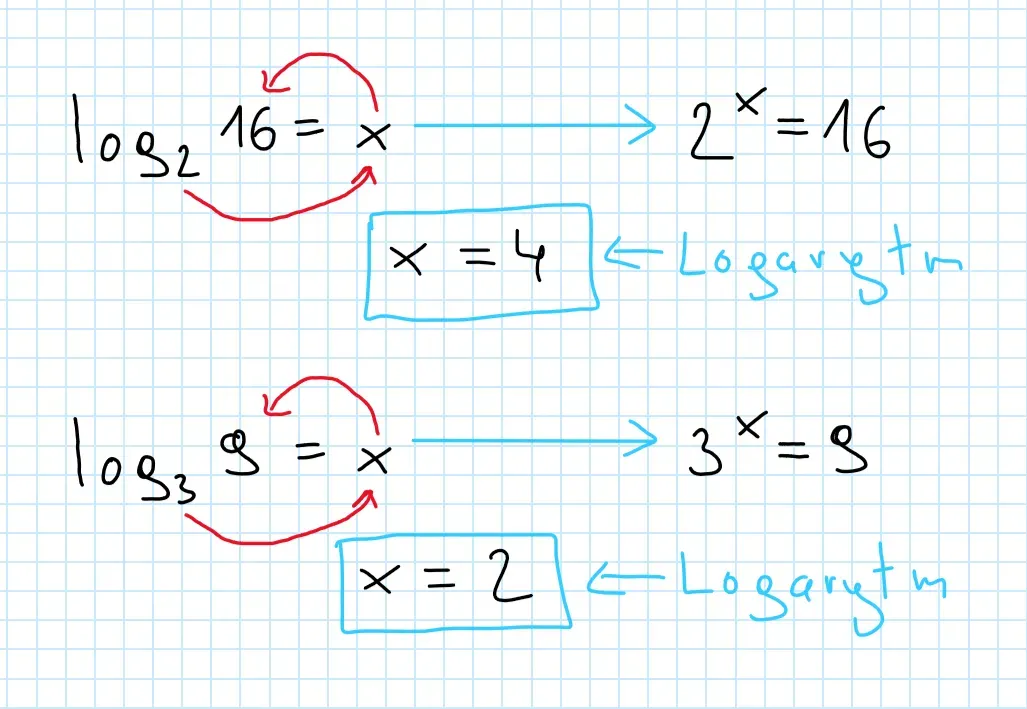
Interpretacja wyników obliczeń logarytmicznych jest kluczowa dla zrozumienia ich znaczenia w praktyce. Po pierwsze, warto pamiętać, że logarytm z liczby mniejszej od 1 zawsze będzie wartością ujemną. To ważne, ponieważ może to wpłynąć na dalsze obliczenia i analizy. Z drugiej strony, logarytm z liczby większej od 1 będzie dodatni, co może wskazywać na wzrost w kontekście analizowanych danych.
Przy interpretacji wyników obliczeń logarytmicznych, warto również zwrócić uwagę na podstawę logarytmu. W zależności od tego, czy używamy logarytmu dziesiętnego, naturalnego czy innej podstawy, wyniki mogą się znacznie różnić. Zrozumienie, jak różne podstawy wpływają na wartości logarytmów, jest istotne dla ich prawidłowej analizy. Wreszcie, zawsze dobrze jest podwójnie sprawdzić obliczenia, aby upewnić się, że wyniki są dokładne i mają sens w kontekście problemu, który rozwiązujemy.
Praktyczne zastosowania logarytmów w analizie danych
Logarytmy mają szerokie zastosowanie w analizie danych, a ich umiejętne wykorzystanie może znacząco poprawić jakość podejmowanych decyzji. Na przykład, w analizie statystycznej, logarytmy mogą być używane do przekształcania danych, co pomaga w eliminacji wpływu ekstremalnych wartości. Dzięki temu, analitycy mogą lepiej zrozumieć rozkład danych i wyciągać bardziej wiarygodne wnioski. Wykorzystanie logarytmów w modelach regresji może również przyczynić się do poprawy dokładności prognoz, szczególnie w przypadkach, gdy relacje między zmiennymi są nieliniowe.
W kontekście przyszłych trendów, rosnąca popularność analizy big data i uczenia maszynowego stwarza nowe możliwości dla zastosowania logarytmów. Wiele algorytmów uczenia maszynowego, takich jak drzewa decyzyjne czy sieci neuronowe, korzysta z logarytmicznych funkcji aktywacji, co pozwala na lepsze modelowanie złożonych zależności w danych. W miarę jak technologia się rozwija, umiejętność efektywnego wykorzystywania logarytmów w analizie danych stanie się kluczowym atutem dla specjalistów w różnych dziedzinach, w tym finansach, marketingu i naukach przyrodniczych.





