Układ figur w piramidkach jest fascynującym zagadnieniem matematycznym, które pozwala zrozumieć, jak liczby i kształty mogą współistnieć w harmonijny sposób. W piramidkach, liczba figur w danym polu jest sumą dwóch pól w piętrze niższym. Ta zasada nie tylko pokazuje, jak można zbudować złożone struktury, ale także ilustruje podstawowe zasady matematyki, które są obecne w wielu dziedzinach życia.
W artykule przyjrzymy się bliżej tej zasadzie, analizując, jak liczba figur w piramidkach jest powiązana z poziomami oraz jakie przykłady ilustrują tę regułę. Zrozumienie tej logiki jest kluczowe dla każdego, kto chce zgłębić tajniki matematyki i jej zastosowań w praktyce.
Kluczowe wnioski:- W piramidkach liczba figur w danym polu jest sumą figur z dwóch pól poniżej.
- Układ figur w piramidkach można zobrazować za pomocą prostych wizualizacji.
- Matematyczne wzory pomagają w precyzyjnym obliczaniu liczby figur w różnych poziomach piramidy.
- Zasady układu figur w piramidkach mają zastosowanie w edukacji, pomagając uczniom w nauce matematyki.
- Przykłady praktycznych zastosowań zasad piramidkowych można znaleźć w architekturze i projektowaniu.
Zasada układu figur w piramidkach i jej znaczenie w matematyce
W matematyce zasada układu figur w piramidkach jest kluczowym elementem, który pozwala zrozumieć, jak liczby i kształty są ze sobą powiązane. Każda figura w piramidzie jest ułożona w taki sposób, że liczba figur w danym polu jest sumą figur znajdujących się w dwóch polach na piętrze niższym. To proste, ale zarazem eleganckie podejście do organizacji figur sprawia, że piramidki stają się nie tylko interesującym zagadnieniem matematycznym, ale także praktycznym narzędziem do nauki.
Znajomość tej zasady ma istotne znaczenie, ponieważ pozwala na rozwijanie umiejętności logicznego myślenia i rozwiązywania problemów. Wiele złożonych struktur matematycznych opiera się na podobnych zasadach. Zrozumienie, jak liczba figur w piramidkach jest powiązana z poziomami, otwiera drzwi do bardziej skomplikowanych koncepcji matematycznych i może być zastosowane w różnych dziedzinach, takich jak architektura czy informatyka.
Jak liczba figur w piramidkach jest powiązana z poziomami
W piramidkach, liczba figur na każdym poziomie jest ściśle powiązana z figurami znajdującymi się na poziomach niższych. Na przykład, jeśli na dolnym poziomie znajdują się 3 figury, a na drugim poziomie 2 figury, to na górnym poziomie będzie ich 5. To zjawisko pokazuje, jak struktura piramidki opiera się na prostych zasadach dodawania, które można łatwo zrozumieć i zastosować.
Relacja ta nie tylko pomaga w wizualizacji układu figur, ale także ułatwia zrozumienie bardziej skomplikowanych koncepcji matematycznych. Wizualizacja tej zasady może być niezwykle pomocna dla uczniów, którzy dopiero zaczynają swoją przygodę z matematyką. Przykłady piramidkowe mogą być wykorzystywane w różnych kontekstach, co sprawia, że nauka staje się bardziej angażująca i zrozumiała.
Przykłady ilustrujące zasady ułożenia figur w piramidkach
Istnieje wiele interesujących przykładów, które ilustrują zasady ułożenia figur w piramidkach. Jednym z najpopularniejszych przykładów jest układ liczb w trójkącie Pascala, gdzie każda liczba jest sumą dwóch liczb znajdujących się bezpośrednio nad nią. Ta struktura matematyczna doskonale obrazuje, jak zasady układu figur w piramidkach mogą być zastosowane w praktyce, a także w nauce.
Innym ciekawym przykładem jest gra logiczna znana jako "piramida liczb", w której gracze muszą umieścić liczby w odpowiednich polach, aby spełnić zasady dodawania. Uczniowie często korzystają z takich gier, aby lepiej zrozumieć zasady matematyczne i rozwijać umiejętności logicznego myślenia. Te przykłady pokazują, jak zasady ułożenia figur w piramidkach mogą być wykorzystywane w różnych kontekstach edukacyjnych.
- Trójkąt Pascala – układ liczb, gdzie każda liczba jest sumą dwóch liczb powyżej.
- Gra "piramida liczb" – logiczna gra, w której gracze muszą umieścić liczby zgodnie z zasadami dodawania.
- Piramida binarna – struktura, w której liczby są organizowane w formie piramidy, a każda liczba jest sumą dwóch liczb poniżej.
- Układ figur w matematycznych łamigłówkach – zadania, które wymagają zrozumienia zasad układu figur w piramidkach.
- Wizualizacje w edukacji – wykorzystanie diagramów piramidowych do nauczania zasad matematycznych.
Analiza matematyczna układu figur w piramidkach
Analiza matematyczna układu figur w piramidkach opiera się na zrozumieniu, jak liczby i figury są ze sobą powiązane. Podstawową zasadą jest to, że liczba figur w danym polu piramidki jest sumą figur w dwóch polach znajdujących się bezpośrednio poniżej. Ta zasada jest nie tylko interesująca, ale także praktyczna, ponieważ pozwala na tworzenie złożonych struktur na podstawie prostych reguł matematycznych.
W matematyce, analiza ta może obejmować różne aspekty, takie jak liczba poziomów w piramidzie oraz ich wpływ na całkowitą liczbę figur. W miarę jak dodajemy kolejne poziomy, liczba figur w piramidzie rośnie w sposób geometryczny, co wymaga zastosowania odpowiednich wzorów do obliczeń. Zrozumienie tych zasad jest kluczowe dla dalszej analizy bardziej skomplikowanych problemów matematycznych.
Wzory matematyczne stosowane do obliczeń w piramidkach
W matematyce istnieje kilka wzorów, które są używane do obliczenia liczby figur w piramidkach. Jednym z podstawowych wzorów jest wzór rekurencyjny, który mówi, że liczba figur na poziomie n jest równa sumie figur na poziomach n-1 i n-2. Oprócz tego, można również wykorzystać wzory kombinatoryczne, które pozwalają na obliczenie liczby sposobów, w jakie figury mogą być rozmieszczone w piramidzie.
| Wzór | Opis |
|---|---|
| F(n) = F(n-1) + F(n-2) | Wzór rekurencyjny dla obliczania liczby figur na poziomie n w piramidzie. |
| C(n, k) = n! / (k!(n-k)!) | Wzór kombinatoryczny do obliczania liczby kombinacji figur w piramidzie. |
Jak wizualizacje pomagają zrozumieć układ figur
Wizualizacje odgrywają kluczową rolę w zrozumieniu układu figur w piramidkach. Wizualne przedstawienie danych, takich jak schematy czy diagramy, pozwala uczniom lepiej uchwycić zasady rządzące tymi strukturami. Dzięki nim, abstrakcyjne koncepcje stają się bardziej namacalne i łatwiejsze do przyswojenia. Na przykład, wykorzystanie diagramów piramidowych może pomóc w zobrazowaniu, jak liczby w poszczególnych polach są ze sobą powiązane.
Różne typy wizualizacji, takie jak modele 3D czy interaktywne aplikacje, mogą znacznie zwiększyć zaangażowanie uczniów. Te narzędzia nie tylko ułatwiają naukę, ale także sprawiają, że proces edukacji staje się bardziej atrakcyjny. Uczniowie, którzy mają możliwość pracy z wizualizacjami, często lepiej rozumieją zasady matematyczne i są bardziej skłonni do eksploracji bardziej skomplikowanych zagadnień.
Czytaj więcej: Kto odkrył Afrykę? Niezwykłe historie odkrywców i ich osiągnięcia
Zastosowanie zasad układu figur w edukacji i praktyce
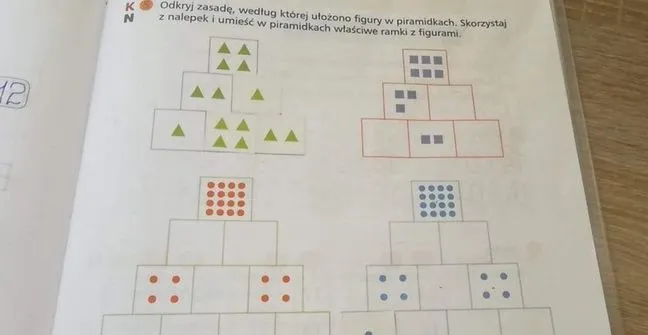
Zasady układu figur w piramidkach mają szerokie zastosowanie w edukacji oraz w różnych dziedzinach praktycznych. W edukacji, te zasady pomagają uczniom w zrozumieniu podstawowych koncepcji matematycznych oraz rozwijaniu umiejętności logicznego myślenia. Uczniowie mogą wykorzystać te zasady do rozwiązywania problemów oraz w kontekście gier edukacyjnych, które angażują ich w naukę przez zabawę. Przykładowo, piramidki mogą być używane w ćwiczeniach z dodawania i mnożenia, co sprawia, że nauka staje się bardziej interaktywna.
Poza edukacją, zasady te znajdują zastosowanie w różnych dziedzinach, takich jak architektura, projektowanie oraz informatyka. W architekturze, zasady te mogą być wykorzystywane do planowania i budowy struktur, które są zarówno estetyczne, jak i funkcjonalne. W informatyce, podobne zasady mogą być stosowane w algorytmach do optymalizacji procesów. Zrozumienie układu figur w piramidkach otwiera drzwi do innowacyjnych rozwiązań w wielu branżach.
Jak zasady piramidkowe mogą być wykorzystane w nauczaniu
Wykorzystanie zasad piramidkowych w nauczaniu może być bardzo efektywne. Nauczyciele mogą wprowadzać różnorodne metody, które angażują uczniów w proces nauki poprzez aktywne uczestnictwo. Na przykład, nauczyciele mogą organizować zajęcia, w których uczniowie tworzą własne piramidki z figur, co pozwala im na praktyczne zastosowanie zdobytej wiedzy. Tego typu aktywności rozwijają umiejętności współpracy i komunikacji w grupie.
Innym skutecznym podejściem jest wykorzystanie gier planszowych, które bazują na zasadach piramidkowych. Gry te mogą być dostosowane do różnych poziomów zaawansowania uczniów, co sprawia, że są odpowiednie zarówno dla dzieci, jak i dorosłych. Dzięki temu, uczniowie mogą rozwijać swoje umiejętności matematyczne w przyjemny i angażujący sposób.
- Tworzenie modeli piramid z materiałów plastycznych, aby zrozumieć zasady ułożenia figur.
- Gry planszowe oparte na zasadach piramidkowych, które angażują uczniów w naukę przez zabawę.
- Warsztaty, w których uczniowie rozwiązują problemy matematyczne przy użyciu piramid.
- Interaktywne aplikacje edukacyjne, które ilustrują zasady ułożenia figur w piramidkach.
- Projekty grupowe, w których uczniowie tworzą własne zadania matematyczne oparte na piramidkach.
Przykłady praktycznych zastosowań zasad w różnych dziedzinach
Zasady układu figur w piramidkach mają również szerokie zastosowanie w różnych dziedzinach poza edukacją. W architekturze, zasady te mogą być używane do projektowania budynków, które są zarówno estetyczne, jak i funkcjonalne. Na przykład, wiele nowoczesnych budynków wykorzystuje formy piramidalne, które są stabilne i optymalizują przestrzeń. Dzięki zrozumieniu zasad układu figur, architekci mogą tworzyć innowacyjne i zrównoważone projekty.
W dziedzinie informatyki, zasady te mogą być stosowane w algorytmach do analizy danych oraz w strukturach baz danych. Na przykład, struktury danych w formie drzew binarnych mogą być używane do organizacji informacji w sposób, który ułatwia ich przetwarzanie. Dzięki zastosowaniu zasad piramidkowych, programiści mogą optymalizować swoje aplikacje i zwiększać ich wydajność. Takie zastosowania pokazują, jak matematyczne zasady mogą mieć praktyczne znaczenie w różnych branżach.
- Architektura budynków w kształcie piramidy, które oferują lepszą stabilność i estetykę.
- Wykorzystanie zasad piramidkowych w algorytmach analizy danych w informatyce.
- Projektowanie efektywnych struktur baz danych opartych na drzewach binarnych.
- Tworzenie modeli matematycznych w inżynierii, które opierają się na zasadach ułożenia figur.
- Optymalizacja procesów produkcyjnych przy użyciu zasad matematycznych.
Nowe technologie w nauczaniu zasad układu figur w piramidkach
W miarę jak technologia wkracza w świat edukacji, pojawiają się nowe możliwości nauczania zasad układu figur w piramidkach. Wykorzystanie rozszerzonej rzeczywistości (AR) oraz wirtualnej rzeczywistości (VR) może zrewolucjonizować sposób, w jaki uczniowie uczą się o tych strukturach. Dzięki tym technologiom, uczniowie mogą interaktywnie eksplorować piramidki w trójwymiarowej przestrzeni, co pozwala im lepiej zrozumieć relacje między figurami oraz zasady ich układania w praktyce.
Co więcej, platformy edukacyjne oparte na sztucznej inteligencji mogą dostosowywać program nauczania do indywidualnych potrzeb uczniów, oferując spersonalizowane ćwiczenia i zadania. Tego typu innowacje mogą nie tylko zwiększyć zaangażowanie uczniów, ale także poprawić ich wyniki w nauce, ponieważ umożliwiają praktyczne zastosowanie zasad matematycznych w wirtualnym środowisku. W przyszłości, integracja tych technologii w edukacji może znacząco wpłynąć na rozwój umiejętności logicznego myślenia i rozwiązywania problemów wśród młodych ludzi.

